The number that didn't understand maths

For the long-suffering professionals who teach maths

IMPARTIAL, JUST, WELL-BALANCED AND RATIONAL. All these adjectives suited our hero down to the ground. He found fame and fortune when he gave King Solomon himself a hand with that highly successful division a few thousand years ago. Since then his reputation has preceded him and he has never been short of work. Even today no Solomonic judgement can be taken seriously if it does not involve the number 2. Ever since that first, crucial decision, life had been so generous, pleasant and uncomplicated that for some years he had given himself up to easy living and idleness. He had even stopped studying maths. To be frank, now that nobody can hear us, he could hardly remember any of the little mathematics he had managed to learn so long ago. This was not something that particularly bothered him. "I'm not doing so badly without all that arithmetic!" he used to say, half in jest, to his numerous fans.

Nevertheless, all was not hunky-dory. Not everyone had such a good opinion of number 2. For instance, his inseparable companion in the sequence of natural numbers was not too fond of him: he was fed up to the back teeth of having to share so many moments of glory with him, of knowing that whatever he did, number 2 would always do twice as much without having to make the slightest effort. And on top of this, despite knowing so much about maths, he was incapable of dividing, whereas that number 2 could divide with an elegance that was quite extraordinary. Sick and tired, number 1 was consumed with rancour and malice and, although a confirmed recluse, he arranged to see a friend -another number 1 like him- who he sometimes met to make an 11, as is right and proper. Between them they cooked up a plan to play a trick on number 2, which would pay him back for being so arrogant.

The pair of ones put their plan into action during the mid-morning break when, for a while, everybody forgot about academic mathematics and the old blackboard where calculations were performed. They went off in search of number 2 and, as nicely as they could, they said:

-We've found a geometric figure. We're going to have a lot of fun. But if we really want to have a good time, there has to be three of us. Why don't you come along?

Number 2 was always ready for a good time so it didn't take them too long to convince him. And you didn't have to be an Einstein of geometry to see that the figure on the blackboard with three sides, two of which were the same length, was a right-angled triangle. Resting on one of the legs, the hypotenuse was the most tempting of slides.

-We're both the same so why don't we take one of the legs each. And you're bigger so you can slide down the longest side. It's really slippery.

Completely unaware of what he was letting himself in for, number 2 didn't think twice. No sooner had they uttered these words than he joyfully launched himself down the hypotenuse. At this point the number ones could not contain a perverse laugh as they saw the God of mathematics, following the dictates of the timetable, enter the scene right on schedule, just as they had expected. Or, at least, he was the god of mathematics in that classroom, the inexorable being who was just as likely to plunge you into the depths of despair with a resounding 0 or raise you to the height of glory with a magnificent 10. In their rather innocent and trivial schoolboy slang, the students referred to this formidable being as "the maths teacher".

-Which of you clumsy oafs is responsible for writing this foolishness on my blackboard? -he roared, outraged. And he grabbed some chalk and angrily drew a square root symbol around number two, who was still happily sliding down the hypotenuse.

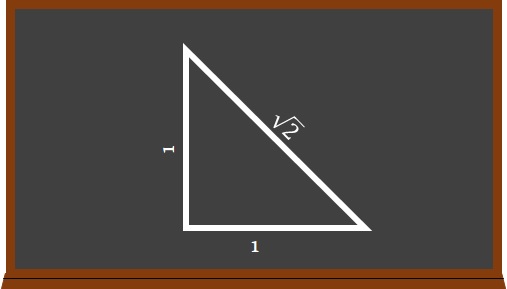
Surprised to find himself suddenly locked up in prison, number 2, who had now been converted into √2, tried with all his might to escape.

-Get me out of here! Help! I promise I'll take maths more seriously in the future, -he sobbed, feeling that he was losing his head, going out of his mind, that he was turning into the first irrational number in the history of maths.

And what about you, dear reader? Are you on your guard? Because if you're not, you may be surprised how many extremely subtle ways there are of getting you inside a square root. Take my word on this. And, just in case, if I were you I would never stop studying ... MATHEMATICS!

Mathematical note

The first mathematician to realise that irrational numbers existed was Hippasus, who studied with Pythagoras 2,500 years ago. Hippasus drew a triangle in which the two legs had a length of 1. When he applied Pythagoras' famous theorem to measure the length of the hypotenuse (the one that states that the sum of the squares of the lengths of each of the triangle's legs is the same as the square of the length of the triangle's hypotenuse) he found that the length was √2, because:

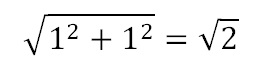
Urbano Lorenzo Seva, Reus 2019

Translation by John F. Bates and Urbano Lorenzo Seva