
El nombre que no sabia matemàtiques
Dedicat als soferts professionals consagrats a la didàctica de les matemàtiques
EQUÀNIME, JUST, PONDERAT I RACIONAL. Tots aquests adjectius li esqueien d'allò més bé al nostre protagonista. La fama i el reconeixement li van arribar en assistir el mateix rei Salomó amb aquella encertada divisió, ara ja fa uns quants milers d'anys. Des de llavors, mai li havia faltat ni feina ni reputació. Encara avui en dia no hi ha decisió salomònica digna de ser considerada seriosament per la qual no sigui requerida la participació indispensable del nombre 2. Es podria dir que, des d'aquella crucial intervenció, la vida havia estat generosa, agradable i fàcil per a ell. Tant era així que feia anys que s'havia deixat emportar per una existència plàcida, sense esforços. Havia, fins i tot, abandonat els estudis de les matemàtiques. Per ser sincers, ara que no ens sent ningú, quasi que ja no recordava res de les poques matemàtiques que algun dia havia arribat a aprendre. No és que n'estigués ni molt menys preocupat ell. "Em va prou bé sense tanta aritmètica!" -acostumava a dir mig en broma als seus innombrables fans.
Tanmateix, no tot eren flors i violes. No tothom estava tan impressionat pel nombre 2 com és això. Sense anar més lluny, el seu company inseparable a la sèrie numèrica no se l'apreciava gaire: estava més que tip de compartir tants pòdiums amb ell; de saber que fes el que fes, aquell altre nombre sempre li doblaria en quantitat sense necessitat de fer cap mena d'esforç. Encara més, ell que tant en sabia de matemàtiques, era incapaç de dividir; mentre que aquell altre nombre ignorant ho aconseguia fer amb una elegància extraordinària. Fart com estava, el nombre 1 es va deixar emportar per la rancúnia i la malícia. Tot i ser un solitari convençut, va resoldre quedar amb un col·lega, un altre nombre 1 com ell, amb qui de tard en tard quedava per fer un onze com cal. Entre tots dos van ordir un pla per jugar-li una mala passada al nombre 2 que tan prepotent semblava als seus ulls.
Aprofitant l'estona d'esbarjo i el corresponent oblit generalitzat del teatre per excel·lència de les matemàtiques acadèmiques, la vella i negra pissarra d'una escola qualsevol, aquell parell de nombres uns van anar a buscar al nombre 2 i li van dir amb to conciliador:
-Hem trobat una figura geomètrica. Ens ho podem passar d'allò més bé. Per gaudir de veritat, però, hem de ser tres. Per què no vens a jugar amb nosaltres?
Sempre disposat al joc fàcil, no va ser menester insistir-li gaire. No calia ser un geni de la geometria per adonar-se que aquella figura de tres costats, dos d'ells d'igual llargada, que estava dibuixada amb guix a la pissarra, era un triangle rectangle. Recolzat com estava sobre un dels catets, la hipotenusa semblava un tobogan d'allò més temptador.
-Nosaltres que som iguals ens posarem aquí als catets i tu, que ets el més gran, llança't pel costat llarg. Ja veuràs com llisca de bé.
Aquell nombre 2 ignorant no va dubtar ni un moment: encara no li havien acabat de dir, que ja es llançava hipotenusa avall desbordant felicitat. Va ser llavors que el parell d'uns no van poder estar-se de fer una rialleta perversa en veure que, rígid com era en els seus horaris, va entrar en escena just a l'hora esperada el Déu de les matemàtiques; si més no el déu de les matemàtiques d'aquella aula: un ser inexorable que amb la mateixa facilitat t'enfonsava a la misèria clavant-te un zero monumental, com t'encimbellava a la glòria infinita amb un magnífic deu. Cal dir que entre els estudiants, fent ús del típic argot escolar d'allò més innocent i trivial, d'aquell ser temible en deien "el profe de mates".
-Qui ha estat el sapastre i ximple que ha gosat escriure aquesta rucada a la meva pissarra? -va cridar tot ofès al mateix temps que agafava un guix i d'un cop de ràbia dibuixava una arrel quadrada al voltant del nombre 2 que encara lliscava tot feliç per la hipotenusa.
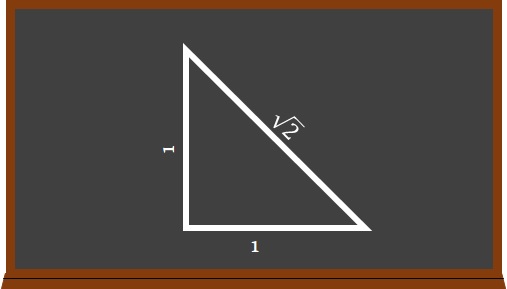
Engabiat per sorpresa dins de la sobtada presó, el nombre 2, ara convertit en el nombre √2, va provar d'escapar-se amb totes les forces, mentre cridava:
-Traieu-me d'aquí! Ajuda! Tornaré a estudiar matemàtiques, ho prometo! -tot ell en un mar de llàgrimes, mentre sentia que se li anava el cap, que perdia el raonament, que es convertia ... en un nombre irracional. El primer nombre irracional de la història de les matemàtiques.
I tu, lector? Ja vigiles? Pensa que en aquesta vida, mentre tu bades, hi ha moltes maneres d'allò més subtils d'encasquetar-te una arrel quadrada com si res, entre broma i broma. Si em vols creure, i per si de cas, jo de tu no deixaria d'estudiar ... MATEMÀTIQUES!
Apunt matemàtic
El primer matemàtic que es va adonar de l'existència dels nombres irracionals va ser Hippasus, que estudiava amb Pitàgores ara fa uns 2.500 anys. Hipassus va dibuixar un triangle on els dos catets són de llargada 1. En aplicar el conegut teorema del seu mestre Pitàgores per mesurar la llargada de la hipotenusa (aquell que diu que la suma dels quadrats dels catets és igual al quadrat de la hipotenusa), Hipassus va obtenir que la llargada era el nombre √2, ja que:
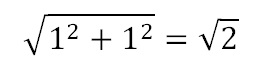
Urbano Lorenzo Seva, Reus 2019